
三相电路二瓦计与三瓦计法功率的测量原理以及接线方法
发布时间:2018-07-02 10:25在三相电路的功率测量中,主要测量方法有二瓦计法和三瓦计法两种方法。对于不同的接线方式场合,应选择恰当的功率测量方式,才能得到准确的功率参数。但是由于部分使用者对于这两种方法适用的场合不够清晰,因此在选择二瓦计或者三瓦计法进行三相功率测试时,极易造成混淆,从而导致选择了错误的测量方法。
那么究竟在什么样的情况下使用两瓦计法,什么样的情况下采用三瓦计法进行三相功率的测量呢?本文从三相电路功率测量的原理角度下分析这两种方法的异同以及分别适用的场合。
二瓦计法
1测量原理
二瓦计法的理论依据是基尔霍夫电流定律,即:在集总电路中,任何时刻,对任意结点,所有流入流出结点的支路电流的代数和恒等于零。也就是说,两根火线的流入电流等于第三根火线的流出电流,或者说,三根火线的电流的矢量和等于零,即:
ia+ib+ic=0 (1)
假设三相负载的中线为N,依据电压的定义:
uab=uan-ubn,ucb=ucn-ubn (2)
三相瞬时功率:
p=uan*ia+ubn*ib+ucn*ic, (3)
将式(1)和式(2)代入式(3),得:
p=uan*ia+(-ubn*ia+ubn*ia)+ubn*ib+ucn*ic
=uab*ia+ubn(ia+ib)+ucn*ic
=uab*ia+ubn(-ic)+ucn*ic
=uab*ia+ucb*ic。
有功功率等于瞬时功率在一个周期内求积分再求平均,得到:
P=P1+P2
P为三相电路有功功率的总和,P1为uab*ia在一个周期内的积分的平均值,P2为ucb*ic在一个周期内的平均值。在正弦稳态电路中:
P=UAB*IA*cosφAB+UCB*IC*cosφCB
即:
P1=UAB*IA*cosφAB
P2=UCB*IC*cosφCB
式中,UAB、IA、UCB、IC均为正弦电压电流的有效值,φAB为UAB和IA的相位差,φCB为UCB和IC的相位差。
从变换的公式中可以看出,采用这种方法进行三相总功率测量时,只需要测量两个电压和两个电流,这就是二瓦计法的推导原理及由来。
二瓦计法测量时,三相电路总功率等于两块功率表的功率之和,每块功率表测量的功率本身无物理意义。
2接线方法
二瓦计法接线示意图如下所示(以测量UabIa,UcbIc为例):
二瓦计法功率表接线示意图
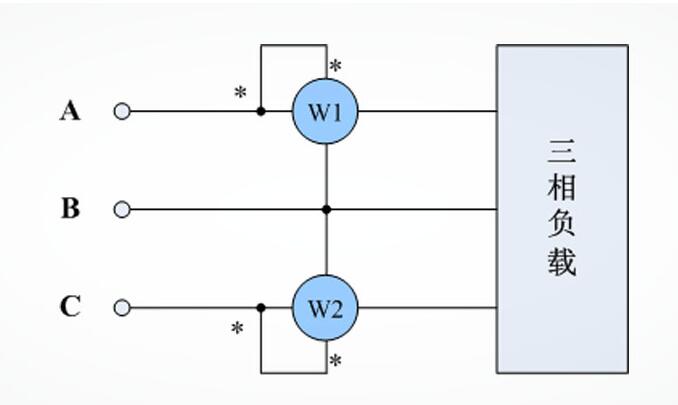
图1中,单相功率表或三相功率表的某一相W1测量的是P1=UAB*IA*cosφAB,W2测量的是P2=UCB*IC*cosφCB。则三相电路总功率为:P=P1+P2。
3适用场合
由于二瓦计法的理论依据是基尔霍夫电流定律,适用于在三相回路中只有三个电流存在的场合,如:
1、 三相三线制接法中线不引出(只能采用两瓦计法);
2、 三相三线制接法中线引出但不与地线或试验相连的场合,与是否三相平衡无关。
三瓦计法
1测量原理
三瓦计法需要将中性点做为电压的参考点,分别测量出三相负载的相电压,相电流,那么三相电路的总功率为三个单相电路的功率之和,每块功率表测量的功率就是单相功率。
如果以瞬时值表示的话,即:
pa=ua*ia,pb=ub*ib,pc=uc*ic,
那么三相瞬时功率:
p=pa+pb+pc,
则三相总有功功率为:
P=PA+PB+PC
在正弦稳态电路中,
PA=UA*IA*cosφA
PB=UB*IB*cosφB
PC=UC*IC*cosφC
其中φA、φB、φC分别为UA与IA、UB与IB、UC与IC的相位差角。
2接线方法
三瓦计法测量接线示意图如下所示:
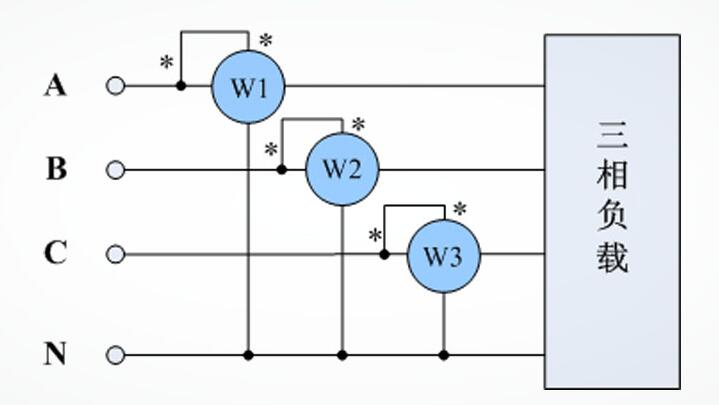
3适用场合
三瓦计法由于需要采用中性点作为电压的参考点,因此适用于如下场合选用:
1、 三相三线制中性线引出,但中性线不与电源或地线连接的场合;
2、 三相四线制,由于无法判断三相负载是否平衡或是否在中性线上有零序电流产生,只能采用三瓦计法;
四误区
1误区一
二瓦计法只适合于三相对称电路的功率测量。
这种说法显然是不正确的。
首先,二瓦计法的证明中,只有ia+ib+ic=0的假设,并没有要求三相对称。
其次,如果三相负载完全对称,那么只需要一个功率表(比如PA)即可得出三相总功率,即P=3PA,二瓦计法也失去了意义。
2误区二
用二瓦计法测量三相四线制的总功率。
由于三相四线制有四个电流(ia、ib、ic和in),而二瓦计法依据的是基尔霍夫电流定律,在三相回路中,三相电流矢量之和必须等于零。但是在三相四线制回路中,会产生零序电流分量,这就使得ia+ib+ic≠0,因此,二瓦计法不适用三相四线制的总功率测量,三相四线制系统应采用三瓦计法。
免责声明: 凡注明来源本网的所有作品,均为本网合法拥有版权或有权使用的作品,欢迎转载,注明出处。非本网作品均来自互联网,转载目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责。