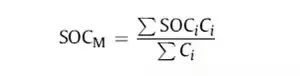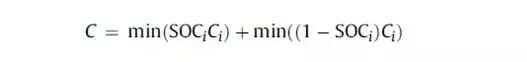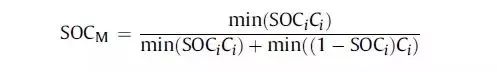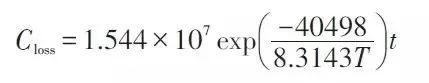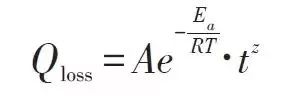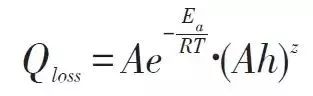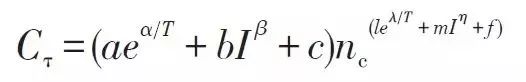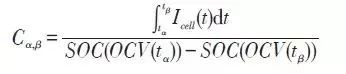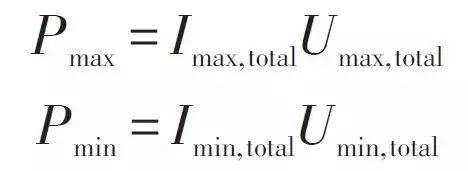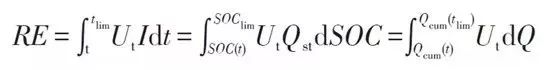详解动力电池管理系统BMS关键技术
发布时间:2018/12/8 19:11:00详解动力电池管理系统BMS关键技术
电池管理系统,BMS(Battery Management System),是电动汽车动力电池系统的重要组成。
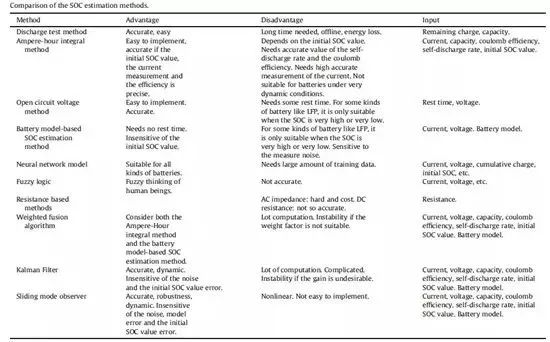
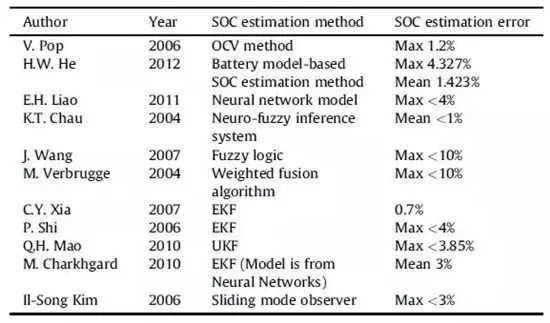
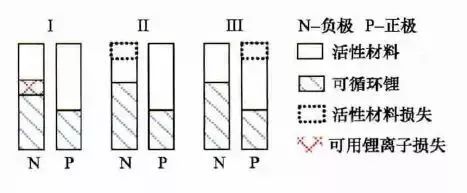
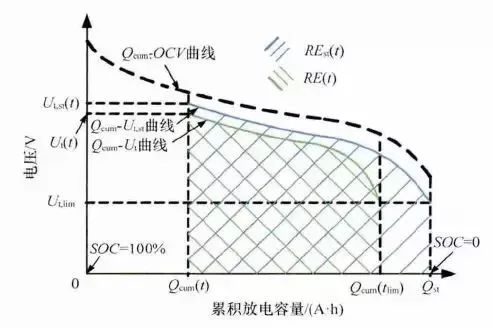
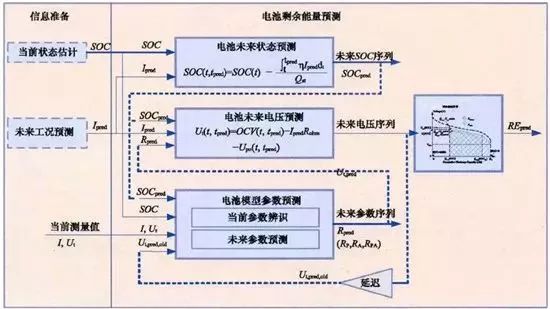
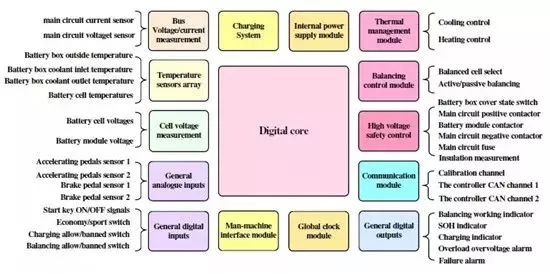
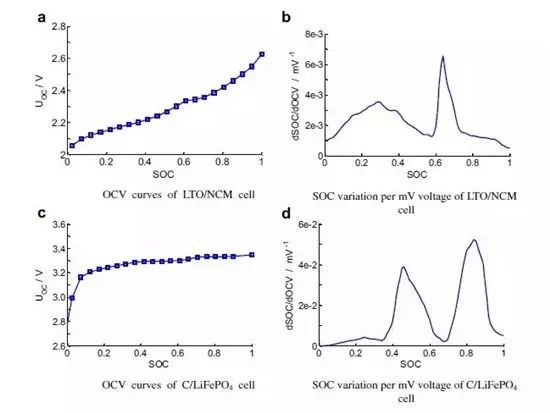
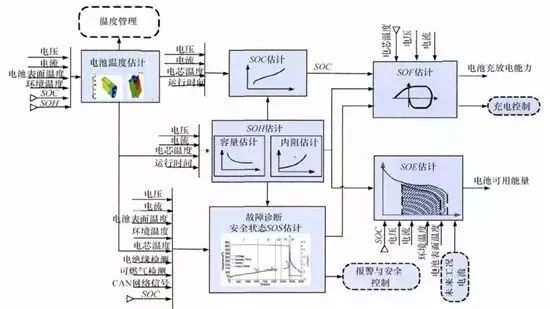
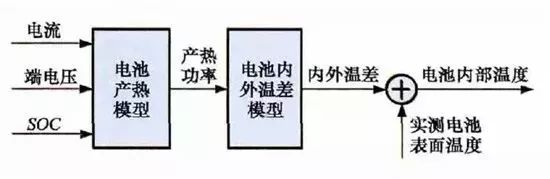
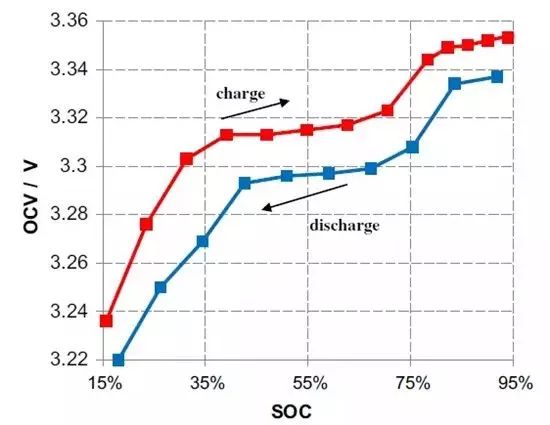
它一方面检测收集并初步计算电池实时状态参数,并根据检测值与允许值的比较关系控制供电回路的通断;另一方面,将采集的关键数据上报给整车控制器,并接收控制器的指令,与车辆上的其他系统协调工作。电池管理系统,不同电芯类型,对管理系统的要求往往并不一样。 那么,一个典型的动力电池管理系统具体都需要关注哪些功能呢?今天翻译整理了一篇文章,一起看看BMS的关键技术。 简 介 电动汽车用锂离子电池容量大、串并联节数多,系统复杂,加之安全性、耐久性、动力性等性能要求高、实现难度大,因此成为影响电动汽车推广普及的瓶颈。锂离子电池安全工作区域受到温度、电压窗口限制,超过该窗口的范围,电池性能就会加速衰减,甚至发生安全问题。 目前,大部分车用锂离子电池,要求的可靠工作温度为,放电时-20~55°C,充电时0~45°C(对石墨负极),而对于负极LTO充电时温度为-30°C; 工作电压一般为1.5~4.2 V左右(对于LiCoO2/C、LiNi0.8Co0.15Al0.05O2/C、LiCoxNiyMnzO2/C以及LiMn2O4/C等材料体系约2.5~4.2 V,对于LiMn2O4/Li4Ti5O12 材料体系约1.5~2.7 V,对于LiFePO4/C 材料体系约2.0~3.7 V)。 温度对锂电池性能尤其安全性具有决定性的影响,根据电极材料类型的不同,锂电池(C/LiMn2O4,C/LMO,C/LiCoxNiyMnzO2,C/NCM,C/LiFePO4,C/LiNi0.8Co0.15Al0.05O2,C/NCA)典型的工作温度如下:放电在-20-55℃,充电在0-45℃;负极材料为Li4Ti5O12 或者 LTO时,充电温度往往可以达到-30℃。 当温度过高时,会给电池的寿命造成不利影响。当温度高至一定程度,则可能造成安全问题。 当温度为90~120 ℃时,SEI 膜将开始放热分解,而一些电解质体系会在较低温度下分解约69℃。当温度超过120℃,SEI 膜分解后无法保护负碳电极,使得负极与有机电解质直接反应,产生可燃气体将。 当温度为130 ℃,隔膜将开始熔化并关闭离子通道,使得电池的正负极暂时没有电流流动。当温度升高时,正极材料开始分解(LiCoO 2 开始分解约在150 ℃,LiNi0.8Co0.15Al0.05O2在约160 ℃,LiNixCoyMnzO2 在约210℃,LiMn2O4 在约265 ℃,LiFePO4在约310℃)并产生氧气。 当温度高于200℃时,电解液会分解并产生可燃性气体,并且与由正极的分解产生的氧气剧烈反应,进而导致热失控。在0℃以下充电,会造成锂金属在负极表面形成电镀层,这会减少电池的循环寿命。 过低的电压或者过放电,会导致电解液分解并产生可燃气体进而导致潜在安全风险。过高的电压或者过充电,可能导致正极材料失去活性,并产生大量的热;普通电解质在电压高于4.5 V时会分解。 为了解决这些问题,人们试图开发能够在非常恶劣的情况下进行工作的新电池系统,另一方面,目前商业化锂离子电池必须连接管理系统,使锂离子电池可以得到有效的控制和管理,每个单电池都在适当的条件下工作,充分保证电池的安全性、耐久性和动力性。 电池管理系统定义 电池管理系统的主要任务是保证电池系统的设计性能,可以分解成如下三个方面: 1)安全性,保护电池单体或电池组免受损坏,防止出现安全事故; 2)耐久性,使电池工作在可靠的安全区域内,延长电池的使用寿命; 3)动力性,维持电池工作在满足车辆要求的状态下。 锂离子电池的安全工作区域如图1所示。 图1为锂离子电池的安全操作窗口 BMS由各类传感器、执行器、控制器以及信号线等组成,为满足相关的标准或规范,BMS应该具有以下功能。 1)电池参数检测。包括总电压、总电流、单体电池电压检测(防止出现过充、过放甚至反极现象)、温度检测(每串电池、关键电缆接头等均有温度传感器)、烟雾探测(监测电解液泄漏等)、绝缘检测(监测漏电)、碰撞检测等。 2)电池状态估计。包括荷电状态(SOC)或放电深度(DOD)、健康状态(SOH)、功能状态(SOF)、能量状态(SOE)、故障及安全状态(SOS)等。 3)在线故障诊断。包括故障检测、故障类型判断、故障定位、故障信息输出等。故障检测是指通过采集到的传感器信号,采用诊断算法诊断故障类型,并进行早期预警。 电池故障是指电池组、高压电回路、热管理等各个子系统的传感器故障、执行器故障(如接触器、风扇、泵、加热器等),以及网络故障、各种控制器软硬件故障等。电池组本身故障是指过压(过充)、欠压(过放)、过电流、超高温、内短路故障、接头松动、电解液泄漏、绝缘降低等。 4)电池安全控制与报警。包括热系统控制、高压电安全控制。BMS诊断到故障后,通过网络通知整车控制器,并要求整车控制器进行有效处理(超过一定阈值时BMS也可以切断主回路电源),以防止高温、低温、过充、过放、过流、漏电等对电池和人身的损害。 5)充电控制。BMS中具有一个充电管理模块,它能够根据电池的特性、温度高低以及充电机的功率等级,控制充电机给电池进行安全充电。 6)电池均衡。不一致性的存在使得电池组的容量小于组中单体的容量。电池均衡是根据单体电池信息,采用主动或被动、耗散或非耗散等均衡方式,尽可能使电池组容量接近于单体的容量。 7)热管理。根据电池组内温度分布信息及充放电需求,决定主动加热/散热的强度,使得电池尽可能工作在最适合的温度,充分发挥电池的性能。 8)网络通讯。BMS需要与整车控制器等网络节点通信;同时,BMS在车辆上拆卸不方便,需要在不拆壳的情况下进行在线标定、监控、自动代码生成和在线程序(程序更新而不拆卸产品)等,一般的车载网络均采用CAN总线技术。 9)信息存储。用于存储关键数据,如SOC、SOH、SOF、SOE、累积充放电Ah数、故障码和一致性等。车辆中的真实BMS可能只有上面提到的部分硬件和软件。每个电池单元至少应有一个电池电压传感器和一个温度传感器。 对于具有几十个电池的电池系统,可能只有一个BMS控制器,或者甚至将BMS功能集成到车辆的主控制器中。对于具有数百个电池单元的电池系统,可能有一个主控制器和多个仅管理一个电池模块的从属控制器。 对于每个具有数十个电池单元的电池模块,可能存在一些模块电路接触器和平衡模块,并且从控制器像测量电压和电流一样管理电池模块,控制接触器,均衡电池单元并与主控制器通信。根据所的数据,主控制器将执行电池状态估计,故障诊断,热管理等。 10)电磁兼容。由于电动车使用环境恶劣,要求BMS具有好的抗电磁干扰能力,同时要求BMS对外辐射小。电动汽车BMS软硬件的基本框架如图2所示。 图2 车载BMS的软硬件基本框架 BMS的关键问题 尽管BMS有许多功能模块,本文仅分析和总结其关键问题。目前,关键问题涉及电池电压测量,数据采样频率同步性,电池状态估计,电池的均匀性和均衡,和电池故障诊断的测量。 1、电池电压测量(CVM) 电池电压测量的难点存在于以下几个方面: 1)电动汽车的电池组有数百个电芯的串联连接,需要许多通道来测量电压。由于被测量的电池电压有累积电势,而每个电池的积累电势都不同,这使得它不可能采用单向补偿方法消除误差。 图3 OCV曲线和每毫伏电压的SOC的变化 2)电压测量需要高(特别是对于C / LiFePO 4 电池)。SOC估算对电池电压提出了很高的要求。这里我们以C / LFP和LTO / NCM型电池为例。 图3显示了电池C / LiFePO 4 和LTO / NCM 的开路电压(OCV)以及每mV电压对应的SOC变化。从图中我们可以看到LTO / NCM的OCV曲线的斜率相对陡峭,且大多数SOC范围内,每毫伏的电压变化对应的SOC率范围低于0.4%(除了SOC 60~70%)。 因此,如果电池电压的测量为10mV,那么通过OCV估计方法获得的SOC误差低于4%。因此,对于LTO / NCM电池,电池电压的测量需要小于10 mV。 但C / LiFePO 4OCV曲线的斜率相对平缓,并且在大多数范围内(除了SOC < 40%和65 ~80%),每毫伏电压的相应SOC变化率达到4%。因此,电池电压的采集要求很高,达到1 mV左右。 目前,电池电压的大部分采集仅达到5 mV。目前,电池的电压和温度采样已形成芯片产业化,表1比较了大多数BMS所用芯片的性能。 表1 统计电池管理和均衡芯片 2、数据采样频率同步性 信号的采样频率与同步对数据实时分析和处理有影响。设计BMS时,需要对信号的采样频率和同步提出要求。但目前部分BMS设计过程中,对信号采样频率和同步没有明确要求。 电池系统信号有多种,同时电池管理系统一般为分布式,如果电流的采样与单片电压采样分别在不同的电路板上;信号采集过程中,不同控制子板信号会存在同步问题,会对内阻的实时监测算法产生影响。同一单片电压采集子板,一般采用巡检方法,单体电压之间也会存在同步问题,影响不一致性分析。 系统对不同信号的数据采样频率和同步要求不同,对惯性大的参量要求较低,如纯电动车电池正常放电的温升数量级为1℃/10 min,考虑到温度的安全监控,同时考虑BMS温度的(约为1℃),温度的采样间隔可定为30 s(对混合动力电池,温度采样率需要更高一些)。 电压与电流信号变化较快,采样频率和同步性要求很高。由交流阻抗分析可知,动力电池的欧姆内阻响应在ms级,SEI膜离子传输阻力电压响应为10 ms级,电荷转移(双电容效应)响应为1~10 s级,扩散过程响应为min级。 目前,电动车加速时,驱动电机的电流从变化到的响应时间约为0.5 s,电流要求为1%左右,综合考虑变载工况的情况,电流采样频率应取10~200 Hz。单片信息采集子板电压通道数一般为6 的倍数,目前最多为24 个。 一般纯电动乘用车电池由约100 节电池串联组成,单体电池信号采集需要多个采集子板。为了保证电压同步,每个采集子板中单体间的电压采样时间差越小越好,一个巡检周期在25 ms内。子板之间的时间同步可以通过发送一帧CAN参考帧来实现。数据更新频率应为10 Hz以上。 包括电池状态包括SOH(健康状态估计)、SOS(安全状态估计)、SOF(功能状态估计)及SOE(可用能量状态估计)。这些功能是期望BMS具备的,但实际应用中,出于客户要求、车型要求以及成本等等的考虑,实际设计到系统中的可能只是其中的几个。 3、电池状态估计 电池状态包括电池温度、SOC(荷电状态估计)、SOH(健康状态估计)、SOS(安全状态估计)、SOF(功能状态估计)及SOE(可用能量状态估计)。 各种状态估计之间的关系如图4所示。电池温度估计是其他状态估计的基础,SOC 估计受到SOH 的影响,SOF 是由SOC、SOH、SOS 以及电池温度共同确定的,SOE 则与SOC、SOH、电池温度、未来工况有关。 图4 BMS状态估计算法框架 3.1 电池温度估计 温度对电池性能影响较大,目前一般只能测得电池表面温度,而电池内部温度需要使用热模型进行估计。常用的电池热模型包括零维模型(集总参数模型)、一维乃至三维模型。 零维模型可以大致计算电池充放电过程中的温度变化,估计有限,但模型计算量小,因此可用于实时的温度估计。一维、二维及三维模型需要使用数值方法对传热微分方程进行求解,对电池进行网格划分,计算电池的温度场分布,同时还需考虑电池结构对传热的影响(结构包括内核、外壳、电解液层等)。一维模型中只考虑电池在一个方向的温度分布,在其他方向视为均匀。二维模型考虑电池在两个方向的温度分布,对圆柱形电池来说,轴向及径向的温度分布即可反映电池内部的温度场。二维模型一般用于薄片电池的温度分析。三维模型可以完全反映方形电池内部的温度场,仿真较高,因而研究较多。 但三维模型的计算量大,无法应用于实时温度估计,只能用于在实验室中进行温度场仿真。为了让三维模型的计算结果实时应用,研究人员利用三维模型的温度场计算结果,将电池产热功率和内外温差的关系用传递函数表达,通过产热功率和电池表面温度估计电池内部的温度,具有在BMS中应用的潜力。图5所示为电池内部温度的估计流程。 图5 电池内部温度估计流程 一般地,锂离子电池适宜的工作温度为15~35℃,而电动汽车的实际工作温度为-30~50℃,因此必须对电池进行热管理,低温时需要加热,高温时需要冷却。热管理包括设计与控制两方面,其中,热管理设计不属于本文内容。 温度控制是通过测温元件测得电池组不同位置的温度,综合温度分布情况,热管理系统控制电路进行散热,热管理的执行部件一般有风扇、水/油泵、制冷机等。 比如,可以根据温度范围进行分档控制。Volt插电式混合动力电池热管理分为3种模式:主动(制冷散热)、被动(风扇散热)和不冷却模式,当动力电池温度超过某预先设定的被动冷却目标温度后,被动散热模式启动;而当温度继续升高至主动冷却目标温度以上时,主动散热模式启动。 3.2 荷电状态(SOC)估计 SOC(State of Charge),可用电量占据电池可用容量的比例,通常以百分比表示,100%表示完全充电,0%表示完全放电。 这是针对单个电池的定义,对于电池模块(或电池组,由于电池组由多个模块组成,因此从模块SOC计算电池组的SOC就像电池电池单体SOC估计模块SOC一样),情况有一点复杂。在SOC估计方法的一节讨论。 目前,对SOC 的研究已经基本成熟,SOC 算法主要分为两大类,一类为单一SOC 算法,另一类为多种单一SOC 算法的融合算法。 单一SOC 算法包括安时积分法、开路电压法、基于电池模型估计的开路电压法、其他基于电池性能的SOC估计法等。融合算法包括简单的修正、加权、卡尔曼滤波(或扩展卡尔曼滤波)以及滑模变结构方法等。 1)放电测试方法 确定电池SOC的最可靠方法是在受控条件下进行放电测试,即指定的放电速率和环境温度。这个测试可以准确的计算电池的剩余电量SOC,但所消耗的时间相当长,并且在测试完毕以后电池里面的电量全部放掉,因此这个方法只在实验室中用来标定验证电池的标称容量,无法用于设计 BMS做车辆电池电量的在线估计。 2)安时积分法 安时积分计算方法为: 式中,SOC 为荷电状态;SOC0为起始时刻(t0)的荷电状态;CN为额定容量(为电池当时标准状态下的容量,随寿命变化);η为库仑效率,放电为1,充电小于1;I 为电流,充电为负,放电为正。 在起始荷电状态SOC0比较准确情况下,安时积分法在一段时间内具有相当好的(主要与电流传感器采样、采样频率有关)。 但是,安时积分法的主要缺点为:起始SOC0影响荷电状态的估计;库仑效率η受电池的工作状态影响大(如荷电状态、温度、电流大小等),η难于准确测量,会对荷电状态误差有累积效应;电流传感器,特别是偏差会导致累计效应,影响荷电状态的。因此,单纯采用安时积分法很难满足荷电状态估计的要求。 3)开路电压(OCV)法 锂离子电池的荷电状态与锂离子在活性材料中的嵌入量有关,与静态热力学有关,因此充分静置后的开路电压可以认为达到平衡电动势,OCV 与荷电状态具有一一对应的关系,是估计荷电状态的有效方法。 但是有些种类电池的OCV 与充放电过程(历史)有关,如LiFePO4/C电池,充电OCV与放电OCV 具有滞回现象(与镍氢电池类似),并且电压曲线平坦,因而SOC估计受到传感器的影响严重,这些都需要进一步研究。 开路电压法的优点是荷电状态估计高,但是它的显著缺点是需要将电池长时静置以达到平衡,电池从工作状态恢复到平衡状态一般需要一定时间,与荷电状态、温度等状态有关,低温下需要数小时以上,所以该方法单独使用只适于电动汽车驻车状态,不适合动态估计。 4)基于电池模型的开路电压法 通过电池模型可以估计电池的开路电压,再根据OCV 与SOC 的对应关系可以估计当前电池的SOC。等效电路模型是最常用的电池模型。 对于这种方法,电池模型的和复杂性非常重要。华等人收集了12个常用等效电路模型,包括组合模型,Rint模型(简单模型),具有零状态滞后模型的Rint模型,具有单态滞后模型的Rint模型,具有两个低通滤波器增强型自校正(ESC)模型,具有四个低通滤波器的ESC模型,一阶RC模型,一个状态滞后的一阶RC模型,二阶RC模型,具有单态滞后的二阶RC模型,三阶RC模型和具有单态滞后的三阶RC模型。 电化学模型是建立在传质、化学热力学、动力学基础上,涉及电池内部材料的参数较多,而且很难准确获得,模型运算量大,一般用于电池的性能分析与设计。 如果电池模型参数已知,则很容易找到电池OCV。然后使用通过实验得出的OCV-SOC查找表,可以容易地找到电池SOC。研究人员使用这种方法,并分别采取RINT模型,一阶RC,二阶RC模型,发现使用二阶RC模型的估计误差是4.3%,而平均误差是1.4%。 图6 充放电C/的LiFePO的OCV曲线4 5)神经网络模型方法 神经网络模型法估计SOC 是利用神经网络的非线性映射特性,在建立模型时不用具体考虑电池的细节问题,方法具有普适性,适用于各种电池的SOC估计,但是需要大量样本数据对网络进行训练,且估算误差受训练数据和训练方法的影响很大,且神经网络法运算量大,需要强大的运算芯片(如DSP等)。 6)模糊逻辑方法 模糊逻辑法基本思路就是根据大量试验曲线、经验及可靠的模糊逻辑理论依据,用模糊逻辑模拟人的模糊思维,最终实现SOC预测,但该算法首先需要对电池本身有足够多的了解,计算量也较大。 7)基于电池性能的SOC 估计法 基于电池性能的SOC估计方法包括交流阻抗法、直流内阻法和放电试验法。交流阻抗法是通过对交流阻抗谱与SOC 的关系进行SOC 估计。直流内阻法通过直流内阻与电池SOC 的关系进行估计。 交流阻抗及直流内阻一般仅用于电池离线诊断,很难直接应用在车用SOC实时估计中,这是因为,采用交流阻抗的方法需要有信号发生器,会增加成本;电池阻抗谱或内阻与SOC 关系复杂,影响因素多(包括内阻一致性);电池内阻很小,车用电池在毫欧级,很难准确获得;锂离子电池内阻在很宽范围内变化较小,很难识别。 8)融合算法 目前融合算法包括简单修正、加权、卡尔曼滤波或扩展卡尔曼滤波(EKF)、滑模变结构等。简单修正的融合算法主要包括开路电压修正、满电修正的安时积分法等。 对于纯电动车电池,工况较为简单,车辆运行时除了少量制动回馈充电外主要处于放电态,站上充电时电池处于充电态,开路电压的滞回效应比较容易估计;电池容量大,安时积分的误差相对较小;充满电的机率大,因此,采用开路电压标定初值和满电修正的安时积分方法可以满足纯电动车电池SOC 的估计要求。 对于混合动力车电池,由于工况复杂,运行中为了维持电量不变,电流有充有放;停车时除了维护外,没有站上充电的机会;电池容量较小,安时积分的相对误差大。因此,简单的开路电压修正方法还不能满足混合动力车电池SOC 的估计要求,需要其他融合方法解决。 加权融合算法是将不同方法得到的SOC 按一定权值进行加权估计的方法。Mark Verbrugge等采用安时积分获得SOCc与采用具有滞回的一阶RC模型获得SOCv的加权方法估计SOC,计算公式为 式中,w为权值。该算法已经在GM混合动力系统中应用。 卡尔曼滤波是一种常用的融合算法。由于SOC不能直接测量,目前一般将两种估计SOC 的方法融合起来估计。SOC被当成电池系统的一个内部状态分析。 又由于电池系统为非线性系统,因此采用扩展的卡尔曼滤波方法,通常采用安时积分与电池模型组成系统进行计算。Plett等研究了安时积分与组合模型、Rint模型(简单模型)、零状态滞回Rint模型、一状态滞回Rint模型、加强自修正模型的卡尔曼滤波融合算法。Wang等研究了安时积分与二阶RC模型的卡尔曼滤波融合算法。 夏超英等研究了安时积分与一阶RC模型的卡尔曼滤波算法,指出EKF作为一个状态观测器,其意义在于用安时积分法计算SOC的同时,估计出电容上的电压,从而得到电池端电压的估计值作为校正SOC 的依据,同时考虑噪声及误差的大小,确定每一步的滤波增益,得到开路电压法在计算SOC 时应占的权重,从而得到SOC 的估计。 这样就把安时积分法和开路电压有机地结合起来,用开路电压克服了安时积分法有累积误差的缺点,实现了SOC 的闭环估计。同时,由于在计算过程中考虑了噪声的影响,所以算法对噪声有很强的抑制作用。这是当前应用最广的SOC估计方法。 Charkhgard等采用卡尔曼滤波融合了安时积分与神经网络模型,卡尔曼滤波用于SOC 计算的是建立合理的电池等效模型,建立一组状态方程,因此算法对电池模型依赖性较强,要获得准确的SOC,需要建立较为准确的电池模型,为了节省计算量,模型还不能太复杂。 Ouyang等提出一种实时性好的基于电化学机理的等效电路模型的SOC 卡尔曼滤波算法,在保证计算速度基础上,提高了SOC 的估计效果,尤其是低SOC 区的估计。但是卡尔曼滤波法的缺点还有卡尔曼增益不好确定,如果选择不好状态将发散。Kim等提出采用滑模技术克服卡尔曼滤波的缺点,据称该方法对于模型参数不确定和干扰具有较强的鲁棒性。 9)电池组SOC 估计 电池组由多节电池串并联组成,由于电池单体间存在不一致性,成组后的电池组SOC 计算更为复杂。由多个电芯并联连接的电池模块可以被认为是具有高容量的单个电池,并且由于并联连接的自平衡特性,可以像单个电池一样估计SOC。 图7 电池模块的无用容量和剩余容量 在串联连接条件下,粗略的估计电池模块的SOC也可以像单体电池一样,但考虑到电池的均匀性,情形会有些不同。假设电池模块中每个单体电池的容量和SOC是已知的。如果有一个非常高效且无损的能量均衡装置,则电池模块的SOC: 其中,SOCM 表示电池模块的SOC,SOCi 表示第i个电池单元的SOC,Ci 表示第i个电池单体的容量。如果平衡装置不是那么有效,真正的电池模块的SOC与该平衡装置的实际性能有关。 如果只有耗散式的被动均衡功能或者没有均衡功能,则电芯中存在一部分无法利用的容量如图6所示,并且随着电池差异性的加剧,这种浪费的容量的比例会越来越大。因此,电池模块的容量表示为: 电池模块可用容量表示为: 电池模组的荷电状态表示为: 由此,在每一节电池单体SOC 都可估计的前提下,就可以得到电池组的SOC 值。要获取单体的SOC值,最直接的方法就是应用上述SOC 估计方法中的一种,分别估计每一个单体的SOC,但这种方法的计算量太大。 为了减小计算量,部分文献在估计电池成组的SOC 方法上做了一些改进研究。Dai 等采用一个EKF 估计电池组平均SOC,用另一个EKF 估计每个单体SOC 与平均SOC 之差ΔSOC。估计ΔSOC 的EKF中需要估计的状态量只有一个,因此算法的计算量较小。 另外,考虑到ΔSOC 的变化很慢,采用双时间尺度的方法可以进一步减小计算量。Zheng等提出了一种M+D模型,即一个相对复杂的电池单体平均模型M,和一个简单的单体差异模型D,利用二乘法计算单体与“平均单体”之间的差值ΔOCV,通过ΔSOC 与ΔOCV 的关系,可以计算每个单体的SOC 值。 表2 各种SOC估计方法比较 表3 不同SOC估计方法的SOC估计误差 表2中比较了不同的SOC估算算法。表3总结了每种方法的SOC估计误差。 综合比较上述常用的SOC 估计方法,卡尔曼滤波等基于电池模型的SOC 估计方法可靠,配合开路电压驻车修正是目前的主流方法。 3.3 健康状态(SOH)估计 健康状态是指电池当前的性能与正常设计指标的偏离程度。电池老化是电池正常的性能衰减,不能完全代表其健康状态。而目前多数SOH 的定义仅限于电池老化的范畴,没有真正涉及电池的健康状况(如健康、亚健康、轻微问题、严重问题等),因此目前的算法应该称为寿命状态。 耐久性是当前业界研究热点,表征电池寿命的主要参数是容量和内阻。一般地,能量型电池的性能衰减用容量衰减表征,功率型电池性能衰减用电阻变化表征。为了估计电池的衰减性能,首先要了解电池的衰减机理。 锂电池衰减机理。锂离子电池为“摇椅式”电池,正负极的活性材料可以看作容纳锂离子的两个水桶,锂离子相当于桶里的水。电池的性能衰减可以理解为“水”变少(即活性锂离子损失),或“桶”变小(正极或负极活性物质变少)。 导致活性锂离子损失的主要原因是:电极与电解液副反应形成钝化膜(如SEI膜);由于充放电电池膨胀收缩疲劳导致电极龟裂,导致电极与电解液副反应形成新的SEI膜,消耗锂离子;不当充电导致的析锂与电解液反应消耗锂离子。 导致活性材料损失的主要原因包括:材料中的锰、铁或镍等离子溶解;活性材料颗粒脱落;活性材料晶格塌陷。目前SOH 估计方法主要分为耐久性经验模型估计法和基于电池模型的参数辨识方法。 锂离子电池双水箱模型 1)耐久性经验模型估计法 耐久性经验模型估计法是基于电池耐久性测试数据标定获得的模型,直接预测容量衰减和内阻的变化。电池的耐久性模型可以分为耐久性机理模型和耐久性外特性模型,两者的主要区别在于,前者侧重于对电池内部副反应机理的研究,并以SEI膜内阻、离子浓度等微观量为观测对象;而后者从试验规律出发,重点关注电池循环过程中表现出来的容量衰减与内阻增加。 有文献根据正负极衰老机理,基于循环锂离子损失机理以及电池内部的材料腐蚀机理,建立了电池SEI膜内阻增加模型以及循环衰减后的端电压模型。由于详细的锂离子电池衰减机理十分复杂,目前还很难准确确定模型的参数,同时运算量也较大,一般不用于车用电池管理中。 基于电池外特性的模型,已经有较多文献涉及,最常见的性能衰减模型是基于Arrhenius规律的模型。Toshiba的手册中给出了钴酸锂电池贮存寿命模型 式中,Closs为容量损失百分比,%;T 为温度,K;t 为时间,月。Bloom等进行了不同环境温度下电池衰减率的试验与分析,试验了以温度为加速应力的电池容量衰减模型,讨论了电池容量保持率与环境温度和循环时间的关系,提出 式中,Qloss 为阻抗增加率(area specific impedance ,ASI)或输出功率,W/s或W;A 为常数;Ea为反应活化能,J;R 是气体常量,J/(mol·K);T 是温度,K;t是时间,h;z 是时间模态,简单情况下可取1/2。其中A、Ea/R、z 都可以通过试验数据用拟合的方法得到。 Wang等基于Bloom等的工作,提出了以Ah 循环总量为变量的双因素模型,将放电倍率乘入原有的时间项,得到以温度和放电倍率为加速应力的电池寿命模型,实现了双应力加速下20%以内的预测误差,即 式中,Qloss为容量损失百分比,%;Ah 为安时循环总量,Ah;其他参数的定义与前面公式相同。 Matsushima研究了大型锂离子电池的性能衰减,发现容量的衰减与时间呈1/2次方关系,即Qloss=Kf×t^(1/2),并发现容量衰减在30%以内时的系数Kf与容量衰减大于30%时的系数Kf不相同。前者较大,说明前30%容量衰减的速度快。Kf服从阿伦尼乌斯定律。进一步地,基于Arrhenius模型的扩展模型,如黎火林、苏金然根据对钴酸锂电池循环寿命的试验,提出了如下的Arrhenius扩展模型: 式中,Cτ为容量衰减率,%;nc为充放电循环寿命,次;T 为温度,K;I 为放电电流,A;a、b、c、l、m、f、α、β、λ、η均为常数,可以通过试验拟合确定。 Li等考虑了电池寿命的多个影响因素,如环境温度、放电倍率、放电截止电压、充电倍率和充电截止电压等,提出了基于耦合强度判断和多因素输入的寿命建模方法(模型中温度的影响也参考了Arrhenius建模方法、电物理量的影响参考逆幂规律),并基于模型的因素敏感性分析了各因素对电池寿命影响的权重,耐久性模型对电池寿命的预测误差为15%以内。 Han等在分析电池性能衰减基础上,认为以石墨为负极的锂离子电池的性能衰减主要是因为负极SEI膜增厚消耗活性锂离子,正常的SEI膜增厚消耗的锂离子与时间呈1/2次方关系,但一般电池存在疲劳龟裂消耗了更多的活性锂离子,因此性能衰减与时间的关系大于1/2 次方。 基于Arrhenius模型建立了4款以石墨为负极的锂离子电池的性能衰减离散模型,并提出基于该离散模型的闭环参数修正方法,经过几次容量修正后,模型参数趋于稳定。 其他外特性建模方法还有神经网络模型,如Jungst等在研究以LiNi0.8Co0.15Al0.05O2为正极材料的电池贮存寿命时建立的神经网络模型。借鉴机械疲劳研究成果,Safari等采用机械疲劳研究中常用的Palmgren-Miner(PM)法则预测电池容量在简单和复杂工况下的衰减情况,并与损害时间累计法(capacity-lossaccumulation over time,LAT)进行比较,结果表明PM法好于LAT法。 2)基于电池模型参数辨识法 参数辨识方法主要基于已有的电池模型,采用状态估计技术,如二乘法、卡尔曼滤波等算法,根据运行的数据,对电池模型参数如容量、内阻等进行辨识,从而获得电池的寿命状态。 Plett将内阻和容量作为系统状态参数,构建了内阻估计状态方程和容量估计状态方程。采用扩展的双卡尔曼滤波方法获得内阻和容量。Gould也基于卡尔曼滤波方法和线性拟合方法辨识电池模型中的容量,继而获得容量随运行循环数的衰减情况。 还有将电池等效电路模型中的内阻视为低频阻抗,采用滑模控制技术进行辨识。Remmlinger介绍了一种用于混合动力车的电池内阻在线辨识方法,为了实现在线应用,改进了二阶RC模型,然后基于特殊的负载信号(发动机启动时的短暂电压及电流),采用线性二乘法获得电池模型的内阻值。Verbrugge认为如果对系统状态参数、测量参数和噪音的演变过程比较了解,采用卡尔曼滤波优化算法来递归辨识是有代表性的方法。 如果缺乏对状态参数、测量参数、噪音的全面了解,采用具有时间指数遗忘因子的加权递推二乘法将是一个较为务实的方法。Wang发现Verbrugge采用叠加积分计算电压的电池模型递推算法在采样频率较高时变得不是很稳定。据此改进了电池模型的算法,并同样也采用指数遗忘因子的加权递推二乘法辨识电池参数(开路电压及内阻等)。 Chiang采用线性或非线性系统控制中常用的自适应控制方法,建立了基于电池等效电路模型的参数估计框架,其中为了便于采用自适应控制技术,锂离子电池等效电路模型采用状态方程来描述,可用于在线监测电池内阻及OCV,分别用于确定SOH 和SOC。Einhorn根据ΔSOC=ΔAh/C 的关系,估计容量的大小,方法为: 式中,任意两个时刻(α,β)的SOC 由OCV 查表得到,该方法可在实际中应用,可以取若干个点,两两搭配计算出多个容量值,再取平均值或中位数。这种方法比较简单,但关键在于OCV 能否辨识。 3)电池组SOH 估计 在不进行均衡的条件下,电池组的容量衰减将远大于单体的容量衰减,郑岳久等提出用两维散点图解释电池组容量衰减的机理,指出电池组的容量衰减量为剩余充电电量单体的容量损失与单体间负极的活性锂离子损失差异之和。为了得到电池组的容量,需要首先获得单体的容量。单体容量获取可以通过上述基于模型参数的辨识方法获得,也可以通过充电电压曲线变换方法获取。 3.4 功能状态(SOF)估计 估计电池SOF 可以简单认为是在估计电池的可用功率。一般而言,电池的可用功率受到电流、电压、SOC、温度等参数的限制,还与电池的老化程度、故障状态等有关。常用的SOF 估计方法可以分为基于电池MAP图的方法和基于电池模型的动态方法两大类。 1)基于MAP图算法 基于电池测试(通常为HPPC测试)数据和、电压限制,可以获得在不同SOC 下的充放电功率。在不同温度、不同衰减程度下进行电池测试,可以建立充放电功率与温度、SOC、SOH 的关系,得到充放电功率MAP图。基于MAP图,实车BMS可以通过插值得到电池的充放电功率,实现SOF 估计。 Do等分别研究了不同SOC、温度、累计放电容量下的充放电功率,并建立了充放电功率的函数解析式,实现了对SOF 的预测。基于MAP图的估计方法简单直接,但需要存储多维MAP图,并且只考虑了静态特性,而对动态工况下的充放电功率估计有一定的局限性。 2)基于电池模型的动态算法 根据电池模型,综合考虑电池的电流、电压、SOC、功率等限制,可以得到充放电电流,从而计算得到电池的充放电功率。 韩雪冰根据电池模型,给出不同电流输入情况下电池的端电压情况,通过迭代计算,获得电池单体在电压限制条件下所允许的电流Imax,voltage 和电流Imin,voltage,并且从电池的机理出发,考虑了电池副反应速率限制下的电流,其方法类似于求取端电压限制下的充放电电流。综合考虑上述限制,获得电池单体的电流。 Sun 等分析比较了几种可用功率预测方法,包括HPPC法、SOC 限制法、电压限制法,以及基于动态模型的多参数估计法,并通过HPPC测试得到充放电电阻,基于Rint模型,利用端电压限制,估计电池的充放电功率。但这种方法估计的实际上是瞬时功率。并且由于Rint模型不够,可能过于乐观地估计了功率,还可能引起过充过放。 与前述方法基本相同,Sun等认为若允许的SOC 变化范围很大,计算出的电流可能很大,并不合理,应与其他方法联合使用。 电压限制法考虑在端电压限制下一段时间内的充放电功率,但仍使用了Rint模型,原理上与前述方法类似,只是算法上并没有采用迭代估计的方法,而是基于模型直接计算电流限值。基于动态模型的多参数估计方法实质上是基于Thevenin模型的电压限制法,综合SOC 与电流的限制,进而得到充放电电流。 以上是获得电池单体充放电电流的方法。实车上电池组由众多电池单体组成,由于单体之间存在不一致性,若要单独计算每个电池单体的可用功率,计算量太大, 韩雪冰提出了充、放电关键电池单体的概念,以减少计算量。综合考虑各种限制条件,可以得到最终的电流Imax,total和Imin,total,将Imax,total、Imin,total代入电池模型中可计算得到对应的端电压Umax,total,Umin,total,进一步可以得到充放电功率,即 3.5 剩余能量(RE)或能量状态(SOE)估计 剩余能量(RE)或能量状态(SOE)是电动汽车剩余里程估计的基础,与百分数的SOE 相比,RE 在实际的车辆续驶里程估计中的应用更为直观。 在电动汽车使用过程中,电池的剩余能量(RE)是指以某一工况行驶时,从当前时刻直至电池放电截止过程中,电池累计提供的能量。RE 可以由电池端电压Ut与相应的累积放电容量Qcum组成的坐标系上的面积表示,如下图所示。 电池剩余能量示意图 当前时刻t 的电池端电压为Ut(t),放电截止时刻记为tlim,对应的端电压为电池允许的放电电压Ut(tlim)。当前时刻的荷电状态为SOC(t),已累积的放电容量为Qcum(t)。 放电截止时刻tlim 对应的SOC 和累积容量分别记为SOClim和Qcum(tlim)。图中,端电压变化表示为绿色曲线,曲线下围成的(绿色斜线)面积对应电池当前时刻在此种工况下的剩余能量RE(t),其计算过程对应公式如下。 由于不同的充放电情况对应的端电压响应不同,使得电池在同一时刻t 提供的剩余能量RE(t)也不相同。此处用一组标准电流倍率下的放电情况作对照,标准情况的端电压Ut,st如图中蓝色曲线(Qcum-Ut,st)所示。由电池SOC 和标准放电容量的定义,此时放电截止位置的SOC 值SOClim,st为0,累积放电容量Qcum,st等于电池标准容量Qst。 标准放电工况下对应的剩余能量REst(t)与之前的RE(t)有明显的差距。电池剩余放电能量的差异同样可以由当前的RE(t)与理论上的剩余放电能量(电池开路电压OCV 曲线围成的面积,图中黑色虚线所示)进行比较。 不同放电工况下电池的能量损失不同,因此只有预测某一特定功率需求下的电池电压响应过程,才能获得准确的RE预测值。由于锂离子电池的特点,其电压输出受到很多变量的影响,如当前SOC、温度、衰减程度SOH,因此在能量预测过程中除传统的SOC 估计模型外,还需要一个专门的电压预测模型。 刘光明等提出一种适用于动态工况的电池剩余放电能量预测方法EPM(energy prediction method),如下图所示,该方法基于当前的电池状态和未来的电流输入,根据电池模型对未来放电过程的电压变化进行预测,并计算放电过程中的累积能量。预测过程中,根据当前的电压、电流测量值对模型参数进行修正,对端电压序列与RE 的预测结果进行更新。 电池剩余放电能量预测方法(EPM)结构 3.6 故障诊断及安全状态(SOS)估计 故障诊断是保证电池安全的必要技术之一。安全状态估计属于电池故障诊断的重要项目之一,BMS可以根据电池的安全状态给出电池的故障等级。目前导致电池严重事故的是电池的热失控,以热失控为的安全状态估计是最迫切的需求。 导致热失控的主要诱因有过热、过充电、自引发内短路等。研究过热、内短路的热失控机理可以获得电池的热失控边界。Feng等研究了一款三元电池的热失控行为,获得了3个特征温度。Ouyang等研究了一款复合三元材料电池的过充电热失控行为,获得了4个过充电特征阶段。这些研究为电池的安全状态估计提供了基础。 故障诊断技术目前已发展成为一门新型交叉学科。故障诊断技术基于对象工作原理,综合计算机网络、数据库、控制理论、人工智能等技术,在许多领域中的应用已经较为成熟。锂离子电池的故障诊断技术尚属于发展阶段,研究主要依赖于参数估计、状态估计及基于经验等方法(与上述SOH研究类似)。 Bohlen等通过电池内阻模型的在线辨识实现了电池在线诊断。Sun等铅酸电池的健康状态(SOH)上,假设正常状态的恒流充放电电压曲线是光滑的,通过观察其充放电曲线的变化辨识电池组可能存在的故障。电动汽车动力往往由成百上千个电池单体串并联构成,个体之间存在一定的差异,即不一致性。一般地,不一致性服从统计分布规律,这为电池组的故障诊断提供了一种理论依据。 Zheng等建立了一种考虑接触电阻的电池分频模型,以代表低频的电池平均模型研究电池组总体行为,以代表高频的差异模型研究电池组一致性问题,成功辨识了电池组内的接触电阻故障。Ouyang等同样采用分频模型,通过内短路电池造成一致性变差特性来诊断内短路的发生。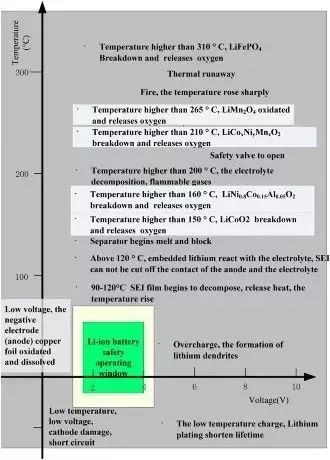
(在25℃测量,休息时间3小时)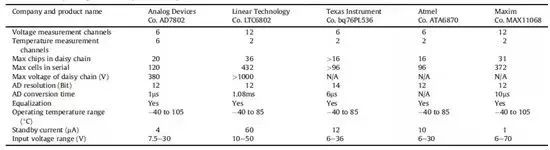
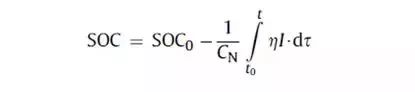
(在25℃测量,休息时间3小时)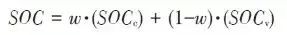
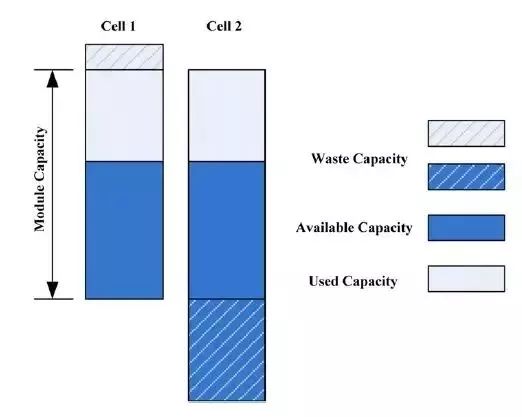
(以2个电池的电池模块为例)