
气象_茎流_辐射_蒸发与植物冠层气孔导度的关系
发布时间:2021/3/26 15:11:00气象_茎流_辐射_蒸发与植物冠层气孔导度的关系
(北京博伦经纬公司)
冠层气孔导度对植物、环境因子的响应规律 , 利用 热脉冲速率法(HPV,heat pulse velocity)或Granier 热消散式探针法对树干液流 ( sap flow) 进行了连续测定 , 计算出整树的蒸腾 , 并由 Penman 2 Monteith 方程得出马占相思的冠层气孔导度值。通过分析 , 发现 : 马占相思冠层气孔导度是控制马占相思树整树蒸腾的主要因素 ; 冠层气孔导度随着水汽压亏缺增加呈负指数函数下降的趋势。使用包括了太阳总辐射、水汽压亏缺和气温的 Jarvis 模型可以较好地模拟马占相思冠层气孔导度对环境因子的响应特征 ; 模拟结果表明 : 环境变量对模型精确度的影响程度依次为 : 水汽压亏缺 > 太阳总辐射 > 气温。
蒸腾是发生在土壤-植被-大气这一复杂统一体间的连续过程 , 也是植物和环境之间物质交换和能量平衡的过程。由于气孔不仅是植物体的水分逸失到空气中的通道 , 也是 CO 2 进入植物体的途径 , 因此蒸腾作用又与植物与大气间碳循环相偶联 , 与植物冠层水分利用效率紧密相关。不仅影响着植物的生长发育 , 而且在一定程度上影响着植物与环境边界层的微气候状况。
冠层气孔导度 (canopy stomatal conductance) 是进行生态、气象和空气质量检测模型模拟时使用的重要参数。在诸多环境因子中 , 光辐射和水汽压亏缺 (vapor pressure deficit) 是驱动冠层气孔导度变化的主要因子 ,气温、土壤水分条件也是影响冠层气孔导度变化的重要因素
冠层气孔导度的测定 , 长期以来多是是利用气孔计或便携式光合系统测定单叶的气孔导度然后经过尺度扩展得到冠层气孔导度值 , 不仅难以获得长期观测值 , 而且在尺度转换和扩展过程中会带来较大的误差。目前随着利用树干液流 ( sap flow) 测定系统观测整树蒸腾技术以及微气象因子观测技术的进步, 可以对冠层
气孔导度进行长期连续的观测。将冠层蒸腾和微气象因子观测值代入 Penman 2 Monteith 方程即可以求出冠层气孔导度值。这种方法在国外多有文献报道 , 已经被成功用于求算针叶树的冠层气孔导度以及温带和热带阔叶树的冠层气孔导度。
本文利用 sap flow 数据结合 Penman 2 Monteith 方程计算冠层气孔导度 , 探讨冠层气孔导度对微气象因子的响应特征并建立经验模型以预测冠层气孔导度的变化 , 旨在为揭示环境因子在冠层水平上对森林生态系统水分利用的影响机理提供理论依据。
监测冠层气孔导度所需的设备
HPV植物茎流计、ATMOS 41气象站和NR LITE2净辐射、HFP01 土壤热通量来测量冠层气孔导度
HPV植物茎流计来测量植物内的水(液)通量。
HPV植物茎流计安装在植物或树木的树干或茎上。通常,传感器安装在表冠下方行李箱的下方。但是,一些实验或假设可能会在主干沿各个位置(例如上分支与下分支或北方对南方)测试冠层电导率。
ATMOS 41气象站来测量大气蒸发需求变量,包括蒸汽压差(VPD),风,太阳辐射,温度和相对湿度。气象站应安装在离被测植物尽可能近的位置,同时仍应遵循有关气象站安装位置的标准协议(即在开放且远离障碍物的地方)。
NR LITE2净辐射传感器来测量环境净辐射Rn数据
HFP01 土壤热通量传感器来测量土壤中的热传导G数据
由 Penman 2 Monteith 方程得出马占相思的冠层气孔导度值
Paudel等人(2015年)提出了一种使用逆Penman-Monteith蒸散方程计算冠层电导的方法。Paudel等人(2015)提出以下方程式来计算冠层电导(G c):
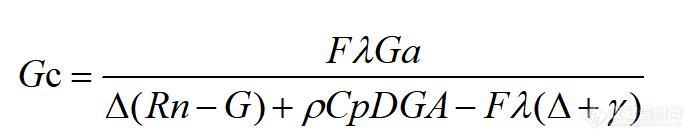
其中F是用HPV植物茎流计测量的液流通量密度(kg m -2 s -1),λ是水的汽化潜热(J kg -1),G a是冠层空气动力学阻力(ms -1)。 ,Δ是水蒸气压力与温度之间的关系的斜率[KPa°C -1 ],ρ是干燥空气的密度(kg m -3)],C p是在恒定压力下干燥空气的比热(J kg -1 C -1),D是蒸气压赤字(KPa),γ是湿度常数(KPa°C -1),R n是净辐射(MJ m -2 s -1),G是土壤热通量(MJ m -2 s -1)。
“平均”气孔的冠层导度
K?stner提出了一种方法来计算整个冠层“平均”气孔的冠层电导率(K?stner等人,1992,1996,2001)。总水蒸气传递电导率(G t)定义为:
G t =(G v * TK)*(E c / D)
其中:
l Gv是水蒸气的气体常数,并且是0.462(m3 kPa-1 kg-1K-1)的常数。
l TK是开氏温度的空气温度(即T + 273.15,其中T是ATMOS 41气象站测得的空气温度)。
l Ec是冠层水流量(kg m -2 s -1),计算为树液总流量,该值由HPV植物茎流计(L/ h)除以每秒的树冠投影面积(m 2)测得。请注意,Ec与F不同,因为针对树冠投影区域校正了Ec,而针对边材区域校正了Fc。
l D是蒸汽压差(kPa)=(610.8 * EXP(17.29 * T /(T + 237.3))/ 1000)*(1-RH),其中RH是相对湿度,是使用ATMOS 41气象站测量的。
l K?stner等人(1992年,2001年)指出,通过减去Ga,Gc与Gt相关,
G a定义为:1/Gc = 1/Gt – 1/Ga
研究人员必须仔细确定Gc或Gt两者的区别,具体取决于是否已通过Gc或Gt方程对数据进行了分析。例如,下面显示的是在夏季一个普通花园中生长的1.5m高,盆栽,礼来的小树苗(Syzygium paniculatum Gaertn。)幼树在30天的测量数据集。数据集包括使用Implexx汁液流量传感器测量的树液流量,通过ATMOS 41气象站测量的天气数据,以及通过上述方程式计算的G c和G t。
(北京博伦经纬公司)
冠层气孔导度对植物、环境因子的响应规律 , 利用 热脉冲速率法(HPV,heat pulse velocity)或Granier 热消散式探针法对树干液流 ( sap flow) 进行了连续测定 , 计算出整树的蒸腾 , 并由 Penman 2 Monteith 方程得出马占相思的冠层气孔导度值。通过分析 , 发现 : 马占相思冠层气孔导度是控制马占相思树整树蒸腾的主要因素 ; 冠层气孔导度随着水汽压亏缺增加呈负指数函数下降的趋势。使用包括了太阳总辐射、水汽压亏缺和气温的 Jarvis 模型可以较好地模拟马占相思冠层气孔导度对环境因子的响应特征 ; 模拟结果表明 : 环境变量对模型精确度的影响程度依次为 : 水汽压亏缺 > 太阳总辐射 > 气温。
蒸腾是发生在土壤-植被-大气这一复杂统一体间的连续过程 , 也是植物和环境之间物质交换和能量平衡的过程。由于气孔不仅是植物体的水分逸失到空气中的通道 , 也是 CO 2 进入植物体的途径 , 因此蒸腾作用又与植物与大气间碳循环相偶联 , 与植物冠层水分利用效率紧密相关。不仅影响着植物的生长发育 , 而且在一定程度上影响着植物与环境边界层的微气候状况。
冠层气孔导度 (canopy stomatal conductance) 是进行生态、气象和空气质量检测模型模拟时使用的重要参数。在诸多环境因子中 , 光辐射和水汽压亏缺 (vapor pressure deficit) 是驱动冠层气孔导度变化的主要因子 ,气温、土壤水分条件也是影响冠层气孔导度变化的重要因素
冠层气孔导度的测定 , 长期以来多是是利用气孔计或便携式光合系统测定单叶的气孔导度然后经过尺度扩展得到冠层气孔导度值 , 不仅难以获得长期观测值 , 而且在尺度转换和扩展过程中会带来较大的误差。目前随着利用树干液流 ( sap flow) 测定系统观测整树蒸腾技术以及微气象因子观测技术的进步, 可以对冠层
气孔导度进行长期连续的观测。将冠层蒸腾和微气象因子观测值代入 Penman 2 Monteith 方程即可以求出冠层气孔导度值。这种方法在国外多有文献报道 , 已经被成功用于求算针叶树的冠层气孔导度以及温带和热带阔叶树的冠层气孔导度。
本文利用 sap flow 数据结合 Penman 2 Monteith 方程计算冠层气孔导度 , 探讨冠层气孔导度对微气象因子的响应特征并建立经验模型以预测冠层气孔导度的变化 , 旨在为揭示环境因子在冠层水平上对森林生态系统水分利用的影响机理提供理论依据。
监测冠层气孔导度所需的设备
HPV植物茎流计、ATMOS 41气象站和NR LITE2净辐射、HFP01 土壤热通量来测量冠层气孔导度
HPV植物茎流计来测量植物内的水(液)通量。
HPV植物茎流计安装在植物或树木的树干或茎上。通常,传感器安装在表冠下方行李箱的下方。但是,一些实验或假设可能会在主干沿各个位置(例如上分支与下分支或北方对南方)测试冠层电导率。
ATMOS 41气象站来测量大气蒸发需求变量,包括蒸汽压差(VPD),风,太阳辐射,温度和相对湿度。气象站应安装在离被测植物尽可能近的位置,同时仍应遵循有关气象站安装位置的标准协议(即在开放且远离障碍物的地方)。
NR LITE2净辐射传感器来测量环境净辐射Rn数据
HFP01 土壤热通量传感器来测量土壤中的热传导G数据
由 Penman 2 Monteith 方程得出马占相思的冠层气孔导度值
Paudel等人(2015年)提出了一种使用逆Penman-Monteith蒸散方程计算冠层电导的方法。Paudel等人(2015)提出以下方程式来计算冠层电导(G c):
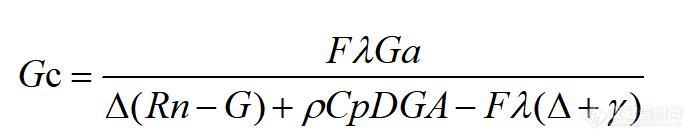
其中F是用HPV植物茎流计测量的液流通量密度(kg m -2 s -1),λ是水的汽化潜热(J kg -1),G a是冠层空气动力学阻力(ms -1)。 ,Δ是水蒸气压力与温度之间的关系的斜率[KPa°C -1 ],ρ是干燥空气的密度(kg m -3)],C p是在恒定压力下干燥空气的比热(J kg -1 C -1),D是蒸气压赤字(KPa),γ是湿度常数(KPa°C -1),R n是净辐射(MJ m -2 s -1),G是土壤热通量(MJ m -2 s -1)。
“平均”气孔的冠层导度
K?stner提出了一种方法来计算整个冠层“平均”气孔的冠层电导率(K?stner等人,1992,1996,2001)。总水蒸气传递电导率(G t)定义为:
G t =(G v * TK)*(E c / D)
其中:
l Gv是水蒸气的气体常数,并且是0.462(m3 kPa-1 kg-1K-1)的常数。
l TK是开氏温度的空气温度(即T + 273.15,其中T是ATMOS 41气象站测得的空气温度)。
l Ec是冠层水流量(kg m -2 s -1),计算为树液总流量,该值由HPV植物茎流计(L/ h)除以每秒的树冠投影面积(m 2)测得。请注意,Ec与F不同,因为针对树冠投影区域校正了Ec,而针对边材区域校正了Fc。
l D是蒸汽压差(kPa)=(610.8 * EXP(17.29 * T /(T + 237.3))/ 1000)*(1-RH),其中RH是相对湿度,是使用ATMOS 41气象站测量的。
l K?stner等人(1992年,2001年)指出,通过减去Ga,Gc与Gt相关,
G a定义为:1/Gc = 1/Gt – 1/Ga
研究人员必须仔细确定Gc或Gt两者的区别,具体取决于是否已通过Gc或Gt方程对数据进行了分析。例如,下面显示的是在夏季一个普通花园中生长的1.5m高,盆栽,礼来的小树苗(Syzygium paniculatum Gaertn。)幼树在30天的测量数据集。数据集包括使用Implexx汁液流量传感器测量的树液流量,通过ATMOS 41气象站测量的天气数据,以及通过上述方程式计算的G c和G t。